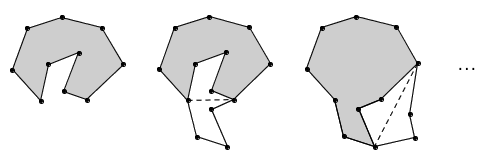
不断把凹的部分翻出来，总能把凹多边形变凸吗？

如图是一个凹多边形，而且凹得相当厉害。一个完美主义者很难容忍这么一个图形，总想着要把凹进去的部分翻出来，把它还原为一个凸多边形。

不幸的是，翻折之后的结果仍然不是凸多边形，图中又产生了新的凹陷。于是，我们想继续把凹进去的部分往外翻，直到整个图形变成凸多边形为止。

问题是，这个过程有完吗？换句话说，我们一定能通过有限多步翻折，把凹多边形变成凸的吗？

这个问题有着非常纠结复杂的历史。这个问题最早可能是由数学家 Paul Erdős 正式提出的。 1935 年，他在 American Mathematical Monthly 上猜想，经过有限步翻折之后，凹多边形一定能变凸。 1939 年， Béla Szőkefalvi-Nagy 给出了一个证明。因此，这个结论又叫做 Erdős-Nagy 定理。有趣的是，这个问题是如此的自然，以至于在此之后，又有一大堆人重新提出并研究了这个问题，而且他们明显并不知道相互之间的已有研究。

这事儿给我们带来的好处就是，我们有了 Erdős-Nagy 定理的好几种截然不同的证明方法。不过，这些证明或者太长，或者太高深，或者又有些漏洞。1999 年， Godfried Toussaint从这些证明中取长补短，给出了一个比较初等的证明。